第二章：谐波¶

在这章中我们会介绍几种新的波形以及他们的频谱，理解频谱的谐波结构（ harmonic structure ），也就是构成整个频谱的正弦信号的集合。

另外，还会介绍在数字信号处理中的另一个重要的概念：混叠（ aliasing ）。然后我会解释一下 Spectrum 是如何工作的。

这章的代码 chap02.ipynb 可以在本书的代码库中找到，你也可以在 http://tinyurl.com/thinkdsp02 查看。

2.1 三角波¶

正弦信号仅包含一个频率分量，因此它的频谱只有一个峰值。大多数复杂的信号，如小提琴声，它们的DFT会包含多个峰值。这一小节，我们来研究这些波形和他们的频谱之间的关系。

我们先从三角波开始，图2.1 展示了一个200Hz的三角波，它的波形看起来像是把正弦信号拉直了。

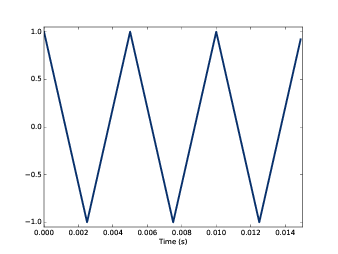
图2.1： 200Hz的三角波波形图

你可以使用 thinkdsp.TriangleSignal 来生成一个三角波:

class TriangleSignal(Sinusoid):

    def evaluate(self, ts):
        cycles = self.freq * ts + self.offset / PI2
        frac, _ = np.modf(cycles)
        ys = np.abs(frac - 0.5)
        ys = normalize(unbias(ys), self.amp)
        return ys

TriangleSignal 继承自 Sinusoid ，因此它同样包含 freq ， amp ， offset 三个属性。不同在于它复写了 evaluate 。其中 ts 依然是采样点的时间，我们来看看这个 evaluate 是如何产生三角波的：

cycles 表示从采样点的循环数。 np.modf 把它的小数部分提取出来放到 frac 中，它的整数部分被丢弃了 [1]
frac 现在是一个给定频率的0~1变化的斜坡信号，将它减去0.5会使其范围变到-0.5~0.5。然后取绝对值后，它的值就成了从0增加到0.5，再从0.5减小到0
unbias 会把整个信号向下移动，使其相对于y轴居中，然后 normalize 将信号的幅度放大到 amp 。

产生图2.1 的代码如下:

signal = thinkdsp.TriangleSignal(200)
signal.plot()

接下来，我们可以用这个信号来产生波形对象，然后再生成它的频谱:

wave = signal.make_wave(duration=0.5, framerate=10000)
spectrum = wave.make_spectrum()
spectrum.plot()

图2.2 显示了频谱图，右面的图在Y轴上进行了放大，这样可以更清晰的显示谐波结构。像我们期望的那样，基频200Hz的幅值是最大的，其它谐波频率分量的峰值出现在200Hz的整数倍频率上。

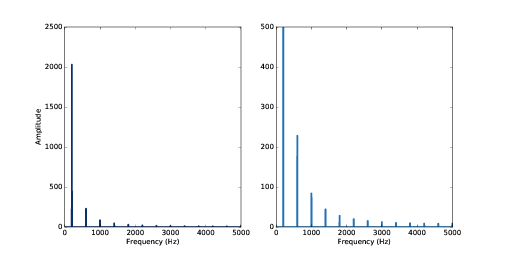
Spectrum of a triangle signal at 200 Hz, shown on two vertical scales. The version on the right cuts off the fundamental to show the harmonics more clearly.

图2.2： 200Hz三角波在不同Y轴坐标尺度下的频谱图。右图中，为了更清除的展示谐波结构，基频的峰值没有全部显示出来

有一个奇怪的现象是：谐波里面没有基频的偶数倍的频率（400Hz，800Hz等），而只有奇数倍的频率（600Hz，1000Hz，1400Hz等）。

这些频率成分的另一个特性是，随着谐波频率的增加，幅度的减弱与频率的平方大致呈比例的关系。例如，600Hz的谐波是基频200Hz的3倍，他的幅度和基频的比例大约是9倍的关系（3的平方）。而1000Hz的谐波是600Hz的1.7倍左右，他们的幅度之比大概是 \({1.7^2} = 2.9\) 。我们把这种关系就称为信号的 谐波结构 。

2.2 方波¶

thinkdsp 还提供了 SquareSignal 类来表示方波信号，这个类的定义如下:

def evaluate(self, ts):
    cycles = self.freq * ts + self.offset / PI2
    frac, _ = np.modf(cycles)
    ys = self.amp * np.sign(unbias(frac))
    return ys

类似 TriangleSignal 和 SquareSignal 这样继承自 Sinusoid 的类，他们的共同点是都具有相同的构造参数：频率，幅度，初始相位。

SquareSignal 的 evaluate 方法也具有类似的结构。其中 ts 依然是采样时间序列， frac 是它的小数部分，它的值从0到1周期的变化。

unbias 将 frac 调整到-0.5~0.5，然后 np.sign 将结果的负值映射到-1，正值映射到1。最后，乘以 amp 将信号的幅值调整到 -amp~amp 。

图2.3 显示了100Hz方波信号的三个周期，图2.4 显示了它的频谱。

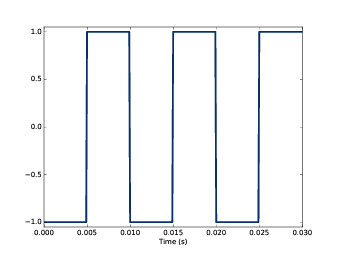
图2.3：100Hz方波信号波形图

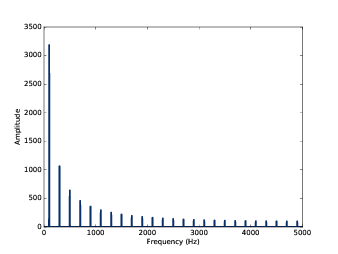
图2.4：100Hz方波信号的频谱图

和三角波一样，方波同样只包含奇数倍的谐波频率，它们的峰值在300Hz，500Hz，700Hz等。但是它们幅度的减弱要比三角波慢一些（不是平方的关系）。

在本章后面的练习题中，你可以看到一些其他的波形和它们的谐波结构。

2.3 混叠¶

坦白说，之前介绍的几个波形，都是我刻意挑选的，避免了比较的复杂的波形和频谱给大家带来困惑。但是，接下来我会介绍一些比较复杂的情况。

图2.5 显示了一个1100Hz的三角信号在10KHz采样率下的频谱。右图是左图的放大后的图像，这样可以看的更清楚。

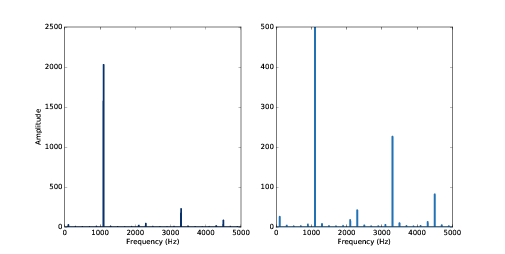
Spectrum of a triangle signal at 1100 Hz sampled at 10,000 frames per second. The view on the right is scaled to show the harmonics.

图2.5：显示了一个1100Hz的三角信号在10KHz采样率下的频谱。右图是左图的放大后的图像

这个信号的谐波应该在3300Hz，5500Hz，7700Hz和9900Hz。图中可以看到我们期望的1100Hz和3300Hz的频率，但是第三个峰值的频率是在4500Hz而不是5500Hz，第四个峰值的频率是在2300Hz而不是7700Hz，下一个峰值的频率是100Hz而不是9900Hz，这是怎么回事呢？

造成这个情况的原因是，在计算整个信号的波形的过程中，实际上是在采样点在对信号进行了离散化的处理，因此在连续信号的各个采样点之间会丢失掉一些信息。对于低频的信号丢失的信息不多，因为同样的采样率下，频率低的信号在一个周期内可以有更多的采样点。

但是如果你用10000Hz的采样率来采集5000Hz的信号，一个信号周期内就仅有两个采样点了。实际上两个采样点是足够的，但是如果信号的频率再高一点，一个周期内采样点小于两个，那么就会产生问题了。

为了解释这个现象，让我们来看两个余弦信号（4500Hz和5500Hz），我们使用10000Hz的采样率来计算他们的波形:

framerate = 10000

signal = thinkdsp.CosSignal(4500)
duration = signal.period*5
segment = signal.make_wave(duration, framerate=framerate)
segment.plot()

signal = thinkdsp.CosSignal(5500)
segment = signal.make_wave(duration, framerate=framerate)
segment.plot()

图2.6 中灰色的线是信号本身，而蓝色的竖线是采样后的信号。对比这两个图，可以发现，两个不同的信号却产生了相同的采样值。

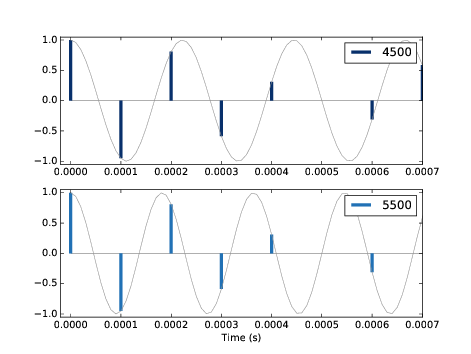
Cosine signals at 4500 and 5500 Hz, sampled at 10,000 frames per second. The signals are different, but the samples are identical.

图2.6：10000Hz采样率下的4500Hz和5500Hz的余弦信号波形图

事实上，当我们用10000Hz采样率对5500Hz信号进行采样的时候，其结果与4500Hz的信号是相同的。正是因为这样，7700Hz的信号和2300Hz的信号，9900Hz的信号和100Hz的信号在采样后也是相同的。

信号采样后产生的这种现象，我们就称为 混叠（aliasing） ，简单来说，就是高频信号采样后的与某些特定的低频信号是无法区分出来的。

在这个例子中（10000Hz采样率），我们最高可以采集的频率为5000Hz，也就是采样率的一半，高于5000Hz的频率成分会被折叠到5000Hz以内，因此我们把这个频率叫做折叠频率（floding frequence），又称为 奈奎斯特频率（Nyquist frequency） 。参见 http://en.wikipedia.org/wiki/Nyquist_frequency 。

我们可以这样来计算折叠后的频率：如果信号的频率大于采样率，通过对信号频率与采样率相除求余，来得到在0到采样率之间的频率，然后如果这个频率大于折叠频率，则用采样率减去这个频率，最后就得到了折叠后的结果。例如，之前波形的第五个谐波频率是12100Hz，求余后为2100Hz，就是折叠后的频率了。你也可以从图2.4 上看到这个2100Hz的频率。同样，也可以看到4300Hz的频率（14300Hz，折叠后为4300Hz）。

2.4 频谱的计算¶

在之前的章节中，我们多次使用了 make_spectrum ，它的代码（省略了一些细节）是这样的:

from np.fft import rfft, rfftfreq

# class Wave:
    def make_spectrum(self):
        n = len(self.ys)
        d = 1 / self.framerate

        hs = rfft(self.ys)
        fs = rfftfreq(n, d)

        return Spectrum(hs, fs, self.framerate)

self 参数代表的是波形对象本身， n 是波形的采样点数目， d 是采样率的倒数，也就是采样时间步长。

np.fft 是Numpy提供的FFT方法（一种高效的计算DFT的算法）。

make_spectrum 使用了 rfft ，它的意思是“实数FFT”，如果信号是实数而不是复数，我们就可以使用它。之后，我们会看到“完整FFT”，它可以处理复信号（见 7.9 ）。 rfft 的结果 hs 是一个复数的Numpy数组，它表示了各个频率分量的复数幅值（幅度和初始相位另一种表示形式）。

rfftfreq 的结果 fs 包含了与 hs 对应的频率值。

对于 hs 中的复数，我们可以这样理解：

复数是实部和虚部的和，通常写成： \(x + iy\) ，其中 \(i\) 是单位虚数，也就是 \(\sqrt { - 1}\) 。我们可以把复数的x和y看做是复数在复平面下的坐标（以实轴为横坐标，虚轴为纵坐标的直角坐标系）
复数也可以表示为幅值和复指数的形式，写成： \(A{e^{i\varphi }}\) ，其中 \(A\) 为模， \(\varphi\) 为幅角。我们可以把它看做是复数在极坐标下的表示。

译者注

\(x + iy\) 的极坐标表示为： \(A\cos (\varphi ) + A\sin (\varphi )i\) ，根据欧拉公式 \({e^{ix}} = \cos (x) + isin(x)\) ，可以得出 \(A{e^{i\varphi }}\)

hs 中的每个复数就代表了该频率分量的复数幅值：它的模值就是该频率的幅度，它的幅角就是该频率的初始相位。

Spectrum 类中提供了两个只读的属性： amps 和 angles ，用来得到这些幅值和初始相位（它们都被放在Numpy数组中）。我们在画频谱图的时候，一般会画出相对于 fs 下的 amps ，或者相对于 fs 的 angles 。在实际使用中，我们几乎不会直接去关注 hs 的实部和虚部。

我们也可以直接通过改变 hs 的值来改变频谱，例如:

spectrum.hs *= 2
spectrum.hs[spectrum.fs > cutoff] = 0

第一行代码将 hs 中的元素乘了2, 相当于将所有谐波的幅值增加了2倍。第二行代码将大于 cutoff 的频率分量的幅值设置到了0。

Spectrum 类中提供了简单的方法来完成这两个操作:

spectrum.scale(2)
spectrum.low_pass(cutoff)

你可以在 http://greenteapress.com/thinkdsp.html 上查看这些方法的文档说明。

至此，你应该对 signal ， Wave 和 Spectrum 这几个类的工作方式有了比较清晰的了解，但我们还没有解释FFT的原理，接下来的几章我们会慢慢的介绍。

2.5 练习¶

下面练习的答案可以参考文件 chap02soln.ipynb 。

练习1 使用 Jupyter 打开 chap2.ipynb ，阅读并且运行上面的代码示例。或者在 http://tinyurl.com/thinkdsp02 浏览和运行它。

练习2 锯齿波的波形是周期性的从-1到1线性变化然后立即下降到-1再循环的一种信号，详见 http://en.wikipedia.org/wiki/Sawtooth_wave 。编写一个锯齿波的类，继承自 Signal ，复写它的 evaluate 方法来生成锯齿信号。

计算出锯齿信号的频谱，看看它的谐波结构和方波，三角波有什么区别。

练习3 生成一个1100Hz的方波信号以及在10000Hz采样率下的波形，画出频谱图，可以看见大部分的谐波被混叠了。那么当你听这个声音的时候，你能听到这些混叠后的频率吗？

练习4 生成任一个信号的频谱，把它的 fs 打印出来，你可以看到他们第一个值是0。也就是说第一个频率分量是0Hz，这代表什么意义呢？试着做如下实验：

生成一个440Hz的三角信号，生成并画出它0.01s的波形。
生成频谱并打印出 hs[0] ，看看他的幅值和初始相位是多少？
设置 hs[0]=100 ，看看这样做会在波形上产生什么样的影响。提示：频谱对象有一个 make_wave 方法可以生成对应的波形。

练习5 写一个函数，接受一个频谱对象作为参数，将 hs 中的每个元素除以 fs 中对应的频率。提示：因为除以0是不可行的，你应该设置 hs[0]=0。用方波，三角波和锯齿波来测试这个函数。

画出原始的频谱图
调用你写的函数，并画出计算得到的频谱图
使用 make_wave 生成这个频谱的波形，并听听看产生了什么效果。

练习6 三角波和方波只有奇次谐波，锯齿波有奇次谐波也有偶次谐波。方波和锯齿波的谐波按照 \(\frac{1}{f}\) 的规律衰减，而三角波的谐波是以 \(\frac{1}{{{f^2}}}\) 的规律衰减。你能找到一个波形它包含奇次和偶次的谐波，并且它们是以 \(\frac{1}{{{f^2}}}\) 的规律衰减吗？提示：有两个方法可以完成这个任务，你可以通过将不同频率的正弦波相加来构造这个波形，或者你也可以从一个类似的信号开始，然后改变它来生成想要的波形。

[1]	使用下划线代表一个变量的时候，表示之后不会使用它，这是一个编码惯例。