第六章：离散余弦变换

本章的主题是 离散余弦变换（Discrete Cosine Transform， DCT） ， 它在MP3和其他格式的音频文件压缩中经常使用，在图像和视频的压缩中也会用到。

DCT与频谱分解时用到的DFT很类似。学习了DCT之后可以更容易的理解DFT。

我们分几个步骤来学习DCT：

1. 先从合成信号开始：给定一组不同频率的余弦信号以及它们的幅值，构造一个合成的信号波形。
2. 使用Numpy来重写合成的函数，这样可以提升计算效率并且为下一步打好基础。
3. 分解信号：给定一个信号和每个频率分量，找到每个频率的幅值。我们先介绍一个简单直接的方法， 但是比较慢。
4. 最后，我们使用一些线性代数的知识来改善计算效率。如果你有线性代数的基础是最好的， 不过没有也没关系，我会把使用到的知识都简单介绍一下。

这章的代码 chap06.ipynb 可以在本书的 代码库 中找到，你也可以在 http://tinyurl.com/thinkdsp06 查看。

6.1 合成

给定一组余弦信号的频率和幅值，我们可以将它们相加来合成一个信号。 在 thinkdsp 模块中， 可以使用 synthesis 函数来完成这个操作:

def synthesize1(amps, fs, ts):
    components = [thinkdsp.CosSignal(freq, amp)
                for amp, freq in zip(amps, fs)]
    signal = thinkdsp.SumSignal(*components)

    ys = signal.evaluate(ts)
    return ys

其中 amps 是幅值， fs 是对应的频率值， ts 是用于计算波形的时间序列。

components 是一组由给定幅值和频率构造的余弦信号， SumSignal 计算出来这些信号的和。

最后，使用 evaluate 计算出了 ts 的信号波形。

可以像下面这样来测试这个函数:

amps = np.array([0.6, 0.25, 0.1, 0.05])
fs = [100, 200, 300, 400]
framerate = 11025

ts = np.linspace(0, 1, framerate)
ys = synthesize1(amps, fs, ts)
wave = thinkdsp.Wave(ys, framerate)

这个例子中，合成信号的频率成分为100Hz的基频和三个谐波频率（100Hz相当于G♯2）。 然后使用合成的信号在11025Hz采样率下生产了波形对象。

虽然像这样合成信号是非常简单的，但是对我们 分解信号 没有什么帮助。 分解信号就是合成的逆操作：给定一个信号，将它分解成不同频率和幅值的余弦信号。

6.2 使用Numpy数组的合成

合成信号的另一个方式是这样:

def synthesize2(amps, fs, ts):
    args = np.outer(ts, fs)
    M = np.cos(PI2 * args)
    ys = np.dot(M, amps)
    return ys

这段代码看上去和之前的完全不同，但是它们实际上完成了相同的事情， 让我们看看它是怎么工作的：

1. np.outer 计算了 ts 与 fs 的 外积（outer product） 。 外积的结果是一个n行m列的矩阵（n为ts的长度，m为fs的长度），其中的每个元素 都是对应位置的时间和频率的乘积 ft 。
2. 将 args 乘以 \(2\pi\) 并应用 np.cos 计算出了 \(\cos (2\pi ft)\) 。也就是说 M 中的每一列都是一个频率分量 在 ts 时间序列下的值。
3. np.dot 计算出了 M 与 amps 的点积，也就是将 amps 的每个值与 M 中每行对应的值相乘并求和。这样就求出了每个时间的合成信号的值。

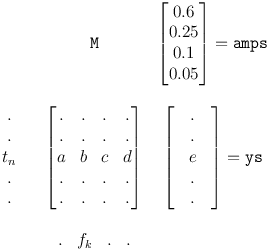
图6.1： 使用Numpy数组的合成过程

图6.1 展示了这个计算的过程。 矩阵 M 的每一行对应了0~1s的时间序列， 其中第n个元素对应的时间用 \({t_n}\) 表示；每一列对应了100~400Hz的频率序列， 其中第k个元素对应的频率用 \({k_n}\) 表示。

我使用了a,b,c,d来表示每一行的四个元素，这里可以得出： \(a = \cos [2\pi (100){t_n}]\)

点积的结果 ys 的每个值对应了 M 的一行，记为 e ，它可以写成：

\[e = 0.6a + 0.25b + 0.1c + 0.05d\]

这样，我们就可以计算出 ys 的所有元素的值，也就是四个频率分量在各个不同时间点下的值与相应 的幅值乘积的和。这就是我们想要的合成结果。

我们可以比较一下两个版本的合成结果是否一致:

ys1 = synthesize1(amps, fs, ts)
ys2 = synthesize2(amps, fs, ts)
max(abs(ys1 - ys2))

可以得出 ys1 和 ys2 最大的差值为 1e-13，这仅仅是浮点数的精度误差。

我们可以用线性代数的形式来描述这个计算过程，如下：

\[\begin{split}M = \cos (2\pi t \otimes f)\\ y = Ma\end{split}\]

这里 a 表示幅值的向量， t 表示时间向量， f 表示频率向量。 ⊗ 表示外积。

6.3 分解

现在我们开始来解决分解的问题。假设给你一个信号并且告诉你这个信号是一组余弦信号合成的。 怎么求出这些余弦信号的幅值呢？换句话说，就是给定 ys ts 和 fs ，求 amps 。

其实，第一步与合成信号是一样，我们先计算出 \(M = \cos (2\pi t \otimes f)\\\) ， 然后就是找到 a 使得 \(y = Ma\) ，也就是解这个线性方程。Numpy提供了 np.solve 来解决这个问题，代码如下:

def analyze1(ys, fs, ts):
    args = np.outer(ts, fs)
    M = np.cos(PI2 * args)
    amps = np.linalg.solve(M, ys)
    return amps

前两行和合成函数是一样，用 ts 和 ys 计算出了 M ，然后使用 np.linalg.solve 计算出了 amps 。

但是这里其实有一个问题，通常解一个线性方程组，需要方程的数量（矩阵的行数）和 未知数的数目（矩阵的列数）相同，也就是说 M 应该是方阵。

但是这个例子中，我们只有四个频率，却有11025个采样时间点，也就是方程的数量比未知数的数量多。

通常情况下，如果 ys 包含的元素超过4个，我们不会只计算4个频率成分。但是在这个例子中， 我们已知了只有这4个频率成分，所有我们可以仅使用 ys 的4个值就可以算出 amps 。

简单起见，我们使用了 ys 的前四个采样值来运行 analyze1 ，如下:

n = len(fs)
amps2 = analyze1(ys[:n], fs, ts[:n])

计算结果确为:

[ 0.6   0.25  0.1   0.05 ]

这个计算方法虽然简单但是很慢，因为解线性方程组的时间复杂度为 \(O({n^3})\) ， n 为 M 的列数。 接下来我们来优化它。

6.4 正交矩阵

求解线性方程组的一个方法是对矩阵求逆。对于方阵 M 来说，逆矩阵表示为 \({M^{ - 1}}\) 使得 \({M^{ - 1}}M = I\) 。 \(I\) 表示单位矩阵，它的对角线元素均为1，其他元素均为0 。

因此，为了求解方程 \(y = Ma\) ，我们将等式两边同时左乘 \({M^{ - 1}}\) 得到：

\[{M^{ - 1}}y = {M^{ - 1}}Ma\]

将右式的 \({M^{ - 1}}M\) 用 \(I\) 代替，得到：

\[{M^{ - 1}}y = Ia\]

因为任何向量左乘单位向量都等于其本身，所以：

\[{M^{ - 1}}y = a\]

也就是说，如果我们求出 \({M^{ - 1}}\) ，就可以使用一个简单的点积来计算出 a 。 这样的时间复杂度仅为 \(O({n^2})\) ，比 \(O({n^3})\) 要好很多。

但是矩阵求逆也比较慢，但是有一些特殊情况比较快的计算出结果。例如如果 M 是正交矩阵， 那么它的逆就是它的转置，记为 \({M^T}\) 。在Numpy中，转置是一个常量时间复杂度的操作， 因为它并没有实际去改变矩阵的元素的位置，而是生成了一个视图，在我们存取元素的时候，实际上 存取的是相应位置转置后的值。

再次强调一遍，正交矩阵的转置与逆相等， \({M^T} = {M^{ - 1}}\) ， 也就意味着 \({M^T}M = I\) 。我们可以使用这个特性来判断一个矩阵是否是正交的。

我们来看看 synthesize2 中的矩阵是不是正交的。在之前的例子中， M 有11025行， 我们需要使用一个更小的版本:

def test1():
    amps = np.array([0.6, 0.25, 0.1, 0.05])
    N = 4.0
    time_unit = 0.001
    ts = np.arange(N) / N * time_unit
    max_freq = N / time_unit / 2
    fs = np.arange(N) / N * max_freq
    ys = synthesize2(amps, fs, ts)

amps 是与之前一样的幅值向量。我们有4个频率成分，因此需要4个采样点就可以了，以保证 M 为方阵。

ts 是从0到1个单位时间的采样时间点序列，这里我随便选了一个0.001s作为单位时间，实际上无论选择什么 样的单位时间，计算结果都是一样的。

我们在单位时间内采样了N个点，奈奎斯特频率应为 N/单位时间/2 ，这里为2000Hz。 fs 为0~2000Hz的 频率序列。矩阵 M 的计算结果为:

[[ 1.     1.     1.     1.   ]
[ 1.     0.707  0.    -0.707]
[ 1.     0.    -1.    -0.   ]
[ 1.    -0.707 -0.     0.707]]

很容易发现，这个矩阵是对称的，也就是说在 (j,k) 位置上的元素与 (k,j) 位置上的元素是相等的， 也就是它的转置与自身相等： \({M^T} = M\) 。

但不幸的是，它不是正交的，因为 \({M^T}M\) 不是单位矩阵:

[[ 4.  1. -0.  1.]
[ 1.  2.  1. -0.]
[-0.  1.  2.  1.]
[ 1. -0.  1.  2.]]

6.5 DCT-IV

但是我们有好几种选择方法，可以使得选择 ts 和 fs 后的 M 是正交的， 因此也就形成了不同的DCT的计算方法。

其中一种方式是将 ts 和 fs 移动半个单位，被称作DCT-IV，“IV”表示罗马数字4， 因为它是8个DCT方法中的第四个。

更新后的代码如下:

def test2():
    amps = np.array([0.6, 0.25, 0.1, 0.05])
    N = 4.0
    ts = (0.5 + np.arange(N)) / N
    fs = (0.5 + np.arange(N)) / 2
    ys = synthesize2(amps, fs, ts)

与之前的代码比较后，你会发现两个改动，一个在 ts 和 fs 上加了0.5的偏移， 二是去掉了 time_unit 从而简化了fs。

结果， M 等于:

[[ 0.981  0.831  0.556  0.195]
[ 0.831 -0.195 -0.981 -0.556]
[ 0.556 -0.981  0.195  0.831]
[ 0.195 -0.556  0.831 -0.981]]

\({M^T}M\) 等于:

[[ 2.  0.  0.  0.]
[ 0.  2. -0.  0.]
[ 0. -0.  2. -0.]
[ 0.  0. -0.  2.]]

由于浮点数精度的原因，其中一些非对焦元素的值被显示为了-0，可以把它当做0来看。 这个矩阵非常接近 \(2I\) 了，也就意味着 M 几乎是正交的，只是多了2倍的因子。 这样已经足够满足我们的需求了。

由于 M 是对称且正交的，因此， M 的逆为 M/2 ，我们可以由此把代码改写为:

def analyze2(ys, fs, ts):
    args = np.outer(ts, fs)
    M = np.cos(PI2 * args)
    amps = np.dot(M, ys) / 2
    return amps

我们把 np.linalg.solve 换成了与 M/2 进行点积。

结合 test2 和 analyze2 ，我们就实现了DCT-IV的计算:

def dct_iv(ys):
    N = len(ys)
    ts = (0.5 + np.arange(N)) / N
    fs = (0.5 + np.arange(N)) / 2
    args = np.outer(ts, fs)
    M = np.cos(PI2 * args)
    amps = np.dot(M, ys) / 2
    return amps

ys 是波形数据，我们不用给定 ts 和 fs ， dct_iv 会通过 ys 的长度来自行计算 ts 和 fs 。

如果之前的推导正确，这个函数应该可以用来对给定的 ys 进行分解求出 amps 。 我们来对它进行一下测试:

amps = np.array([0.6, 0.25, 0.1, 0.05])
N = 4.0
ts = (0.5 + np.arange(N)) / N
fs = (0.5 + np.arange(N)) / 2
ys = synthesize2(amps, fs, ts)
amps2 = dct_iv(ys)
max(abs(amps - amps2))

首先，我们预设了一组幅值 amps ，并计算出了 ts 和 fs ， 然后使用 synthesize2 计算出了合成信号，然后用 dct_iv 对合成信号进行分解， 得到 amps2 。最后，将 amps 与 amps2 比较，他们的最大差值仅为1e-16 （由浮点数精度导致），说明计算正确。

6.6 逆DCT

最后，我们注意到 analyze2 和 synthesize2 的代码几乎是一样的，唯一的区别在于 analyze2 的结果除了2。因此，我们可以这样来计算DCT的逆运算:

def inverse_dct_iv(amps):
    return dct_iv(amps) * 2

inverse_dct_iv 其实就是信号的合成：它把输入幅值向量并输出合成信号 ys 。 我们可以像下面这样测试 inverse_dct_iv

amps = [0.6, 0.25, 0.1, 0.05]
ys = inverse_dct_iv(amps)
amps2 = dct_iv(ys)
max(abs(amps - amps2))

同样，结果最大的差值是1e-16。

6.7 DCT类

thinkdsp 中提供了一个 Dct 类对DCT进行封装（类似于 Spectrum 类对FFT进行的封装）。 我们可以通过波形的 make_dct 来生成Dct对象:

signal = thinkdsp.TriangleSignal(freq=400)
wave = signal.make_wave(duration=1.0, framerate=10000)
dct = wave.make_dct()
dct.plot()

这个一个400Hz的三角波的DCT结果，见 图6.2 。DCT的结果可以是正值也可以是负值， 负值代表的是负的余弦，也就相当于移动了180°的相位。

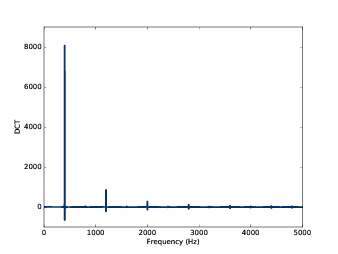
图6.2： 400Hz的三角信号在10kHz采样率下的DCT变换

make_dct 内部用的是DCT-II方法来计算DCT，在 scipy.fftpack 中提供这个方法:

import scipy.fftpack

# class Wave:
    def make_dct(self):
        N = len(self.ys)
        hs = scipy.fftpack.dct(self.ys, type=2)
        fs = (0.5 + np.arange(N)) / 2
        return Dct(hs, fs, self.framerate)

dct 的结果保存在 hs 中，对应的频率值为 fs （见 6.5 DCT-IV ）。 然后使用它们和采样率来生成一个 Dct 对象。

Dct 类也提供了 make_wave 方法来计算逆DCT，我们来测试一下:

wave2 = dct.make_wave()
max(abs(wave.ys-wave2.ys))

wave 和 wave2 的 ys 差别也大概为1e-16（同样是浮点数误差）。

make_wave 使用了 scipy.fftpack.idct

# class Dct
def make_wave(self):
    n = len(self.hs)
    ys = scipy.fftpack.idct(self.hs, type=2) / 2 / n
    return Wave(ys, framerate=self.framerate)

逆DCT默认不会结果进行归一化，因此我们需要除以 2N 。

6.8 练习

下面练习的答案可以参考文件 chap06soln.ipynb 。

练习1 之前我说 analyze1 的时间复杂度是 \(O({n^3})\) ， 而 analyze2 的时间复杂度为 \(O({n^2})\) 。使用不同长度的信号作为输入， 运行这两个函数并计时，看看我这个说法对不对。提示：可以使用魔法命令 %timeit 来计时。

如果你将运行时间和输入数据的长度画在一个对数坐标下，应该可以得到一条直线，对于 analyze1 来说直线的斜率为3，而 analyze2 斜率为2。

用同样的方法测试 dct_iv 和 scipy.fftpack.dct 。

练习2 DCT主要应用在音频和图像的压缩中。简单来说，基于DCT的压缩原理是：

1. 把长段的数据分段。
2. 计算每段的DCT。
3. 把幅值很小的频率成分去掉，保存剩下的频率和幅值。
4. 解压的时候，将频率和幅值进行逆DCT运算。

把这个算法实现一下，并应用到一段音乐或语音上，看看多少频率成分被去除后，解压后的 声音能够感觉到与原始声音有区别。

为了让这个方法更实用，我们需要存储稀疏矩阵（大部分的元素为0）。 Numpy提供了几种方法，参见 http://docs.scipy.org/doc/scipy/reference/sparse.html 。

练习3 本书的 代码库 中有一个 phase.ipynb 的文件，讨论了相位对于声音的感受的影响。 阅读并运行里面的代码，并找一个其他的录音进行试验。你能找到相位结构与声音感觉之间的关系吗？