第八章：滤波和卷积

本章我会介绍信号处理中的一个重要的定理-卷积定理（Convolution Theorem）。 不过在这之前，我们需要先了解一下卷积这个概念。 这里，我们先以一个简单的平滑作为例子开始我们的学习。

这章的代码 chap08.ipynb 可以在本书的 代码库 中找到，你也可以在 http://tinyurl.com/thinkdsp08 查看。

8.1 平滑

平滑是一种试图消除信号短期的变化的操作，信号经过平滑操作后，可以更好的 揭示长期的变化趋势。例如，如果把股票的每日价格变化画出来，它会看起来像噪声一样， 但是经过平滑之后，我们就可以比较清楚的看到他是上升的趋势还是下降的趋势了。

一个最普通的平滑操作就是移动平均法。它将信号之前 n 个时刻的值的平均值作为 新的信号的第 n 个值。

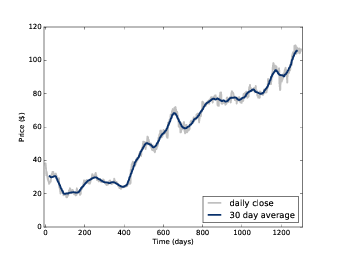
图8.1： Fackbook股票的日线和30日平均线

例如， 图8.1 展示了Fackbook的股票从2012年5月17日到2015年11月8日的每日收盘价格曲线。灰色的曲线代表原始数据， 而蓝色的曲线则是进行了30日移动平均之后的数据。可见，平滑后，信号的短期变化被很大程度的消除了， 这样一来我们也就更容易的看出数据的长期变化趋势。

平滑操作也能用于声音信号。我们先从一个440Hz的方波信号为例，如 2.2 中所述，方波的谐波衰减的 比较慢，它包含很多高频的成分。

我们先生成一个方波信号和它的两段波形:

signal = thinkdsp.SquareSignal(freq=440)
wave = signal.make_wave(duration=1, framerate=44100)
segment = wave.segment(duration=0.01)

wave 是1s的波形， segment 是一个较短的波形（0.01s），我会用它来作图。

为了计算信号移动平均值，我会使用一个类似 3.7 的窗口。在那一章，我们使用了汉明窗来避免 因为信号前后不连续引起的频谱泄露。这里，我们使用窗函数来计算一段信号的加权和。

上例中，我们可以通过一个包含相等且和为1的11个元素的窗，来计算移动平均:

window = np.ones(11)
window /= sum(window)

然后将这个窗应用到波形上:

ys = segment.ys
N = len(ys)
padded = thinkdsp.zero_pad(window, N)
prod = padded * ys
sum(prod)

padded 将窗函数尾部添加0来保证其长度与 segment.ys 一致。这种补0的方法，称为 padding 。

prod 是波形数据与窗函数的乘积， 他们的和其实就是窗口内前11个元素的平均值。 我们需要把窗口滚动到下一个位置。这个例子中，前11个元素都是-1，因此平均值也是-1。

为了计算移动平均的下一个值，我们需要将窗口向右移动一个位置，然后再进行同样的计算:

rolled = np.roll(rolled, 1)
prod = rolled * ys
sum(prod)

使用同样的方法，我们可以计算剩余的所有元素，下面的代码将之前的代码都放到了一个循环中， 这样它就可以循环的处理整段信号并把结果放入了数组中:

def smooth(ys, window):
    N = len(ys)
    smoothed = np.zeros(N)
    padded = thinkdsp.zero_pad(window, N)
    rolled = padded

    for i in range(N):
        smoothed[i] = sum(rolled * ys)
        rolled = np.roll(rolled, 1)
    return smoothed

smooth 就是用来保存结果的数组， padded 就是补0后的窗函数， rolled 是 padded 的一份拷贝，它在每次循环结束后都会右移一个元素。在循环内，我们将 ys 和 rolled 相乘并求和， 然后依次放入 smooth 数组中。

结果见 图8.2 ，其中灰线是原始信号，蓝线是平滑后的信号。可见，平滑后的信号在原始信号突变的时候 是以斜坡的方式变化的，也就是信号的变化没有那么“尖锐”了。

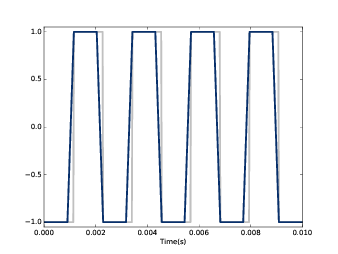
图8.2： 440Hz方波信号（灰线）和11元素的移动平均信号（蓝线）

8.2 卷积

上一节中，我们运用窗函数对信号逐段进行的操作就叫做 卷积（convolution）

卷积是一个经常使用的操作，Numpy中提供了一个更加简单和快速的实现:

convolved = np.convolve(ys, window, mode='valid')
smooth2 = thinkdsp.Wave(convolved, framerate=wave.framerate)

np.convolve 计算了波形和窗函数的卷积。参数 valid 表示只计算窗函数和波形 完全重叠没有交叉的部分，因此它从窗函数与波形数据左对齐开始，直到窗口移动到与波形右对齐。 计算结果与 图8.2 是完全相同的。

严格的来说，之前的代码和它还是有一定的区别，之前的代码计算的是互相关函数：

\[(f \star g)[n] = \sum\limits_{m = 0}^{N - 1} {f[m]g[n + m]}\]

这里 f 代表了长度为 N 的波形数据， g 是窗函数， ⋆ 是互相关的算符。 当计算第n个值的时候，实际上我们需要将 g 右移 n 个位置，这也是 g[n+m] 的意义。

而卷积的定义是：

\[(f * g)[n] = \sum\limits_{m = 0}^{N - 1} {f[m]g[n - m]}\]

\(*\) 是卷积算符，这个式子与之前那个的区别在于 g 的 m 是负的， 也就是 g 的值是反过来的，计算的时候也应该反过来。由于上一个例子中， 窗函数是对称的，因此它们的结果才会一样。如果使用其他的窗函数，就必须要注意这一点。

为什么要像这样来定义卷积呢？有两个原因：

• 这个定义在很多场合下都是很自然而然的得出来的，尤其是在分析信号处理系统的时候， 我们会在第十章的时候学习。
• 这个定义是卷积定理的基础，我们马上就会学习。

之后我们还会学习到循环卷积。

8.3 频域

在时域上，平滑操作会使信号的变化没有那么剧烈，那么在频域上，有什么变化呢？ 让我们先来看看原始信号的频谱:

spectrum = wave.make_spectrum()
spectrum.plot(color=GRAY)

再来看看平滑后的信号频谱:

convolved = np.convolve(wave.ys, window, mode='same')
smooth = thinkdsp.Wave(convolved, framerate=wave.framerate)
spectrum2 = smooth.make_spectrum()
spectrum2.plot()

same 模式表示计算结果需要和输入的长度一致。虽然，这样会产生一些不太好的值， 不过不会应该我们之后的分析。

如 图8.3 所示，基频的幅值几乎没有变化，而接下来几个谐波分量的幅值都有所衰减。 再往高频的分量就几乎被消除了。因此，平滑操作具有低通滤波的效果，见 1.5 频谱 以及 4.4 粉红噪声 。

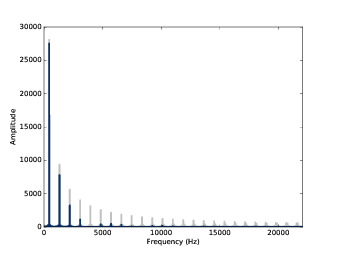
图8.3： 方波平滑前（灰色）和平滑后（蓝色）的频谱图

为了知道各个频率成分衰减的程度，我们计算出了两个频谱分量的比例:

amps = spectrum.amps
amps2 = spectrum2.amps
ratio = amps2 / amps
ratio[amps<560] = 0
thinkplot.plot(ratio)

ratio 就是平滑前和平滑后的幅值比例。 当 amps 很小的时候，这个比例会很大并且没什么意义， 因此我们简单的把它设置为了0 。

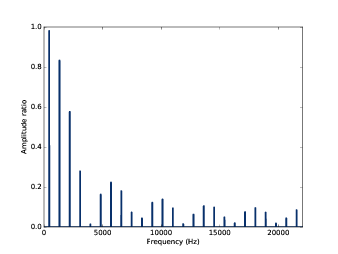
图8.4： 方波平滑前（灰色）和平滑后（蓝色）的幅值比例

如 图8.4 ，在低频的时候 ratio 是比较大的，接近1，然后逐渐减小直到截止频率4000Hz。 但是，在4000Hz之后， ratio 又开始在0~0.2之间变动，这是怎么回事呢？

8.4 卷积定理

答案就是卷积定理，它的数据公式如下：

\[DFT(f * g) = DFT(f) \cdot DFT(g)\]

式中， f 是波形数据， g 是窗函数，也就是说根据卷积定理， f 与 g 的卷积后的信号的DFT， 与它们分别进行DFT然后再相乘的结果是一样的。

由于波形是随时间变化的函数，因此卷积操作是在 时域（time domain） 上进行的。 而DFT后相乘是在 频域（frequency domain） 进行的，因为DFT的结果是频率的函数。 因此，我们又可以这样来描述卷积定理：

• 时域的卷积相当于频域的乘积

这也解释了 图8.4 的结果。当我们把波形和窗函数进行卷积，实际在频域上就是波形的频谱和窗函数频谱的 乘积。为了证明这一点，我们先计算出了窗函数的DFT:

padded = zero_pad(window, N)
dft_window = np.fft.rfft(padded)
thinkplot.plot(abs(dft_window))

padded 是补0后的窗函数， dft_window 是窗函数的DFT。

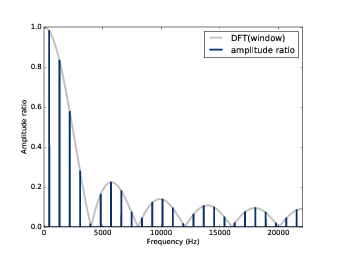
图8.5： 方波平滑前和平滑后的幅值比例以及窗函数的DFT结果

结果见 图8.5 ，平滑前后的幅值比例与窗函数的DFT结果 dft_window 是完全重合的。 用数学公式表示是：

\[|DFT(f*g)|/|DFT(f)| = |DFT(g)|\]

在频域下，窗函数的DFT就称为 滤波器（filter） ，也就是说时域上一个窗函数的卷积，就对应了 频域下的一个滤波器。

8.5 高斯滤波器

上一节使用的移动平均窗是一个低通滤波器，但是滤波的效果并不是很好。因为它的DFT一开始衰减的很快， 但是后面开始上下震荡，这种情况被称为 旁瓣（sidelobes） 。由于移动平均窗实际上是一个方波 信号，它的频谱上包含高频的谐波成分并且幅值是按照 1/f 衰减的，这就比较慢了。

而高斯窗函数就比较好了。Scipy中提供了很多常用的卷积窗函数，其中就包括高斯窗:

gaussian = scipy.signal.gaussian(M=11, std=2)
gaussian /= sum(gaussian)

这里， M 是窗的长度， std 是高斯分布函数的标准差参数。 图8.6 展示了这个窗函数的形状， 它是高斯分布钟型曲线的离散化，图中还画出了移动平均窗的曲线，实际上就是一条平的直线，由于看起来像是 矩形，因此又称为矩形窗。

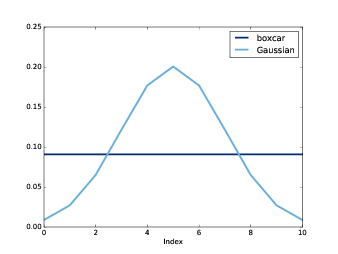
图8.6： 高斯窗函数

我用高斯窗函数重新进行了一次和上一节相同的计算，结果如 图8.7 ，可见通过高斯窗进行平滑后的 频谱衰减比例与高斯窗的DFT是一致的。

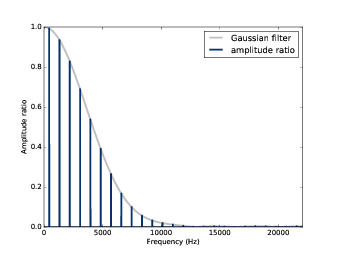
图8.7： 经过高斯窗平滑前后的频谱比例与窗函数的DFT结果

对于低通滤波的效果来说，高斯平滑要比移动平均要更好一些。图中，随着幅值的衰减，几乎没有旁瓣出现，因此它 可以更好的去除信号的高频成分。

我们之前提到过，高斯函数的DFT也是高斯函数，它的频谱是以 \({e^{ - {f^2}}}\) 衰减的，因此，它比 1/f 的矩形窗要好很多。

8.6 高效的卷积

FFT的一个重要的运用是，它与卷积定理结合起来可以提供一种高效的计算卷积，互相关和自相关函数的方法。

这里，我们重新写一次卷积定理的公式：

\[DFT(f * g) = DFT(f) \cdot DFT(g)\]

因此，我们得到一种计算卷积的方法：

\[f*g = IDFT(DFT(f) \cdot DFT(g))\]

IDFT 指的是逆DFT变换。我们之前使用的卷积计算方式，时间复杂度是 \(O({n^2})\) ； 而使用这种方式，时间复杂度仅为 \(O(n\log n)\) 。

为了验证这种方式的正确性，我们将分别使用两种方法来计算 图8.1 中Fackbook股票数据的卷积结果:

import pandas as pd

names = ['date', 'open', 'high', 'low', 'close', 'volume']
df = pd.read_csv('fb.csv', header=0, names=names)
ys = df.close.values[::-1]

上面的代码中使用了Pandas来从csv文件中读取数据，这个文件包含在 代码库 中。 Pandas是一个数据处理库，本书中涉及的不多，因此即使你不太熟悉也没关系。 如果有兴趣和话，可以阅读 Think Stats at http://thinkstats2.com 。

从csv读入的数据保存在 df 中，它是一个 DataFrame 对象（Pandas中的一个数据类）， close 是包含收盘数据的Numpy数组。

接下来，我将高斯窗应用到了这个数据上:

window = scipy.signal.gaussian(M=30, std=6)
window /= window.sum()
smoothed = np.convolve(ys, window, mode='valid')

下面的 fft_convolve 使用FFT来进行卷积:

from np.fft import fft, ifft

def fft_convolve(signal, window):
    fft_signal = fft(signal)
    fft_window = fft(window)
    return ifft(fft_signal * fft_window)

我们将同样的高斯窗补0后，使用 fft_convolve 来进行同样的计算:

padded = zero_pad(window, N)
smoothed2 = fft_convolve(ys, padded)

smooth2 的开头包含 M-1 个无效的数据， M 是窗长度，我们可以像下面这样来去掉这些数据:

M = len(window)
smoothed2 = smoothed2[M-1:]

经过比较， fft_convolve 和 np.convolve 的结果是相同的。

8.7 高效的自相关

在 8.2 卷积 中我提到了互相关的定义，它和卷积之间仅有一个符号的差别。

上一节我们介绍了计算卷积的高效方法，同样，我们也可以高效的计算互相关和自相关。 我们继续使用Facebook的股票数据来计算它的自相关:

corrs = np.correlate(close, close, mode='same')

使用 same 模式使得结果与输入数据 close 的长度一致，相应的 lag 值是从 -N/2 到 N/2-1 。 计算结果见 图8.8 中的灰色曲线。除了 lag 为0的时候以外，没有其他的峰值，表明这个信号没有明显的 周期性。然而，自相关函数下降的比较慢，说明这个信号类似于 5.3 中的粉红噪声。

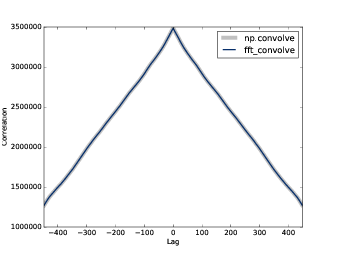
图8.8： 使用 fft_correlate 和 np.correlate 的计算结果

使用卷积来计算自相关之前，我们需要把信号补0到两倍信号的长度，这是因为FFT假定信号值周期的， 而进行自相关的信号使用这个假设是不成立的，因此我们把信号补0，最后再从结果中去掉无效的元素。

考虑到卷积和自相关的公式差一个负号，我们使用 np.flipud 把窗函数（本身）进行反向，再 调用 fft_convolve 计算卷积，最后的结果就是自相关了。 np.flipud 操作并没有真的对 内存进行反向的操作，只是产生了一个反向的视图，因此它的速度是很快的:

def fft_autocorr(signal):
    N = len(signal)
    signal = thinkdsp.zero_pad(signal, 2*N)
    window = np.flipud(signal)

    corrs = fft_convolve(signal, window)
    corrs = np.roll(corrs, N//2+1)[:N]
    return corrs

fft_convolve 的结果长度是2N，其中前 N/2 个元素和后 N/2 个元素是有效的，其余都是由于补0 导致的无效数据，于是我们将它右移并取出了前 N 个元素，也就对应了 lag 从 -N/2 到 N/2-1 的值。 结果如 图8.8 ，两种计算方法得到的结果是相同的。

需要注意的是， 图8.8 中自相关的值是很大的，我们需要将其进行归一化（使值的范围在-1到1之间）， 见 5.6 。

计算互相关也可以使用同样的方法。首先将两个信号信号补0然后将其中一个反向，然后使用上述方法计算卷积，最后再 取出有效的元素。补0和截取有效数据的操作是比较繁琐的，因此Numpy中提供了一些函数来帮助我们完成这项操作。

8.8 练习

下面练习的答案可以参考文件 chap08soln.ipynb 。

练习1 阅读并运行 chap08.ipynb 中的代码。里面有一个交互性的实验来帮助你了解高斯窗中参数的变化 对于截止频率的影响。

当你增大高斯窗的 std 而不改变窗函数的长度 M 的时候，会出现什么问题？

练习2 之前我提到了高斯曲线的傅立叶变换同样是高斯曲线，对于DFT来说，这个结论也是近似正确的。 尝试一下当你改变 std 后，它的DFT有什么变化。

练习3 在第三章中，我们学到了汉明窗和其他的一些窗函数，用于抑制频谱泄露，并且我们通过他们的DFT结果来 了解了它们各自不同的抑制效果。

与之前使用的高斯窗一样，生成一个同样长度汉明窗，补0后画出它的DFT，看看这两种窗函数的低通滤波效果更好？ 你会发现使用y轴对数坐标来画DFT是很有用的。

同样的，使用不同的窗函数和长度来进行这个实验。